Skip to main content

Flow Network | Ford-Fulkerson Algorithm

Flow Network is a directed graph in which each edge has a capacity and each edge receives a flow. 

In this blog, we will discuss the following things:

  • Introduction of: 
    • network, max-flow problem
    • capacity, flow
  • Ford-Fulkerson method
  • pseudo code, residual networks, augmenting paths
  • cuts of networks
Introduction - 
Network

We can understand Network by looking into some examples: liquids flowing in pipes, parts through assembly lines in a factory, the current through electrical network.
Flow Network: Directed graph, G=(V, E)
                        where V is set of vertices,
                                   E is set of Edges.
Max-Flow problem
Max-flow problem is about finding the feasible flow through a flow network and with maximum possible flow rate.
Capacity(of an edge)
Capacity is the maximum limit of flow that edge can allow.
If (u,v) ∉ E ⇒ c(u,v) = 0
Flow
It is the amount that is currently flowing now in an edge.
Flow in G=(V, E) : f: VxV -> R with 3 properties:
  1. Capacity constraint: for all (u,v)∈ V, we need f (u, v) ≤ c (u, v).
  2. Skew Symmetry: For all (u, v) ∈ V, we need f (u, v) = - f (u, v).
  3. Flow Conservation: For all u ∈ V-{s, t}, 
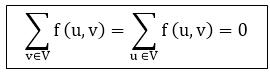
    Flow Networks and Flows
Net flow: Net flow is the positive or negative value of flow f(u,v).
Value of a flow f: It is the amount that can flow in a network.
|f| = Σ f(s, v)

Ford-Fulkerson Method

This algorithm was developed by L. R. Ford, Jr. and D. R. Fulkerson in 1956.
Before understanding this algorithm let us look at the ideas behind this. This algorithm consists of the following three main ideas:
  1. Residual network: The residual network G(f) of flow network G with flow f consists of the same vertices v ∈ V as in G which are linked with residual edges (u,v)∈ E(f) which can admit more positive flow.
    The residual capacity c(f) is the amount of additional net flow f(u,v) before exceeding the capacity c(u,v).
    c(f) (u,v) = c(u,v) – f(u,v)


  2. Augmenting Paths: An augmenting path "p" is a path from s(source) to t(destination) in the residual network G(f). It should be free of the cycle.
    Residual capacity of p: c(f) (p) = min{c(f) (u,v): (u,v) is on p}



  3. Cuts of Flow Network: A cut (S, T) of a flow network G=(V, E) is a partition of V into S and T = V \ S such that s ∈ S and t ∈ T.
Basic Ford Fulkerson algorithm(Pseudo code):
for each edge(u,v) in E
    do f(u, v) = 0
       f(v, u) = 0
while there exists a path p from s to t in residual network G(f)
    do c(f)[p] = min{c(f)(u, v) | (u, v) is in p}
        for each edge (u, v) in p
            do f(u,v) += c(f)[p]
            f(v, u) = -f(u, v)


Labels:

Comments

Post a Comment

Popular posts from this blog

Setting up Cpp environment on VS Code | Windows 10

I have recently switched to Windows 10 from PopOs ( a Debian-based Linux) because of my project-related work which could not be done in any Debian-based Linux. So, I installed windows 10 on my system and it was just a little annoying but cool as well because my system's performance has increased (which was obvious as I have deleted all my previous data just backed up around 60Gb of it). So, starting with the process of setting up the environment for C++ on the VS Code on Windows 10. In Linux, I used to run C++ files on Sublime text only but on Windows, I'm just using VS code for both C++ and JavaScript. Let's start setting up the environment. I am dividing this whole process into 4 steps: First, you have to set up a compiler for the system. As we know that C/C++ is compiled programming language which requires a compiler to make them compiled and run. In Linux, there is already a gcc/g++ compiler preinstalled. But in Windows, you have to install it separately. So you can dow...
Post a Comment
Read more

Cpp program to count digits in an integer

C++ program to count the number of digits in an integer: Suppose you have an integer, n = 1567. The number of digits in n is 4. Input: 1567 Output: 4 Input: 58694 Output: 5 Solution:  To solve this problem, we can simply iterate to all these digits starting from the rightmost digit. We will update the number by dividing it by 10 until it becomes less than or equal to zero. Step 1: n=1567, count=0.               n = n/10; count = count+1; Step 2: n=156, count=1.             n = n/10; count = count+1; Step 3: n=15, count=2.             n = n/10; count = count+1; Step 4: n=1, count=3.             n = n/10; count = count+1; Step 5: n=0; count=3;               Loop will end here. C++ implementation: #include   <bits/stdc++.h> using   namespace   std ; int   main ()...
Post a Comment
Read more

3 hacks to wake up early in the morning

So this is what everyone says that we have to wake up early in the morning. Yes, it's good to wake up early and this could be the best decision you will take in your life.   I have read this somewhere that " If you want to change your life, do nothing just start waking up early in the morning and things will start happening ". So yes waking up early in the morning is going to help you a lot and it will surely help in changing your life. Now the question that arises is how we can wake up early in the morning? We all want to wake up early at 5 or 6 Am in the morning but when the clock hits 5 and your alarm makes the sound, your mind says just 5 minutes more and these 5 minutes end up at 1 hour.  So the question is how can we make it to wake up early in the morning. So in this article, I'm sharing 3 hacks that can surely help you in achieving your goal of waking up early in the morning.  The secret of waking up early doesn't lie in the process of waking up early in ...
6 comments
Read more